Atmospheric lapse rate: Difference between revisions
imported>Milton Beychok m (→Lapse rates and atmospheric stability: Minor copy additions) |
Pat Palmer (talk | contribs) m (Text replacement - "United States" to "United States of America") |
||
| (15 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
{{See also|Earth's atmosphere}} | |||
{{TOC|right}} | {{TOC|right}} | ||
The '''atmospheric lapse rate''' (<sup> </sup><font style="vertical-align:-5%;"><math>\scriptstyle\Gamma</math></font><sup> </sup><sup> </sup>) refers to the change of an atmospheric variable with a change of altitude, the variable being [[temperature]] unless specified otherwise (such as [[pressure]], [[Density (chemistry)|density]] or [[humidity]]).<ref>The lapse rate is often defined as the negative change of temperature with a change of altitude. That definition leads to statements such as "A positive lapse rate indicates cooling as height increases while a negative lapse rate indicates warming as height increases". That is counter-intuitive since lapse rates are usually denoted as a negative number (i.e., – 6.5 K/kilometre or the equivalent 3.6 °F/1000 feet) to indicate cooling with an increase of height.</ref><ref>[http://www.atmos.ucla.edu/~fovell/AS3downloads/lapse_rates.pdf Lapse rates and air parcels] Professor Robert Fovell, Department of Atmospheric and Oceanic Science, [[University of California, Los Angeles]]</ref><ref>[http://rst.gsfc.nasa.gov/Sect14/Sect14_1b.html Characteristics of Air Parcels and Air Masses; Clouds] Dr. Nicholas Short, [[National Aeronautics and Space Administration]] (NASA)</ref> While usually applied to [[Earth's atmosphere]], the concept of lapse rates can be extended to atmospheres (if any) that exist on other planets. | The '''atmospheric lapse rate''' (<sup> </sup><font style="vertical-align:-5%;"><math>\scriptstyle\Gamma</math></font><sup> </sup><sup> </sup>) refers to the change of an atmospheric variable with a change of altitude, the variable being [[temperature]] unless specified otherwise (such as [[pressure]], [[Density (chemistry)|density]] or [[humidity]]).<ref>The lapse rate is often defined as the negative change of temperature with a change of altitude. That definition leads to statements such as "A positive lapse rate indicates cooling as height increases while a negative lapse rate indicates warming as height increases". That is counter-intuitive since lapse rates are usually denoted as a negative number (i.e., – 6.5 K/kilometre or the equivalent 3.6 °F/1000 feet) to indicate cooling with an increase of height.</ref><ref>[http://www.atmos.ucla.edu/~fovell/AS3downloads/lapse_rates.pdf Lapse rates and air parcels] Professor Robert Fovell, Department of Atmospheric and Oceanic Science, [[University of California, Los Angeles]]</ref><ref>[http://rst.gsfc.nasa.gov/Sect14/Sect14_1b.html Characteristics of Air Parcels and Air Masses; Clouds] Dr. Nicholas Short, [[National Aeronautics and Space Administration]] (NASA)</ref> While usually applied to [[Earth's atmosphere]], the concept of lapse rates can be extended to atmospheres (if any) that exist on other planets. | ||
| Line 6: | Line 6: | ||
Lapse rates are usually expressed as the amount of temperature change associated with a specified amount of altitude change, such as 9.8 [[Kelvin|K]] per [[kilometre]], 0.0098 K per [[metre]] or the equivalent 5.4 [[Fahrenheit and Rankine temperatures|°F]] per 1000 [[U.S. customary units|feet]]. If the atmospheric air cools with increasing altitude, the lapse rate may be expressed as a negative number. If the air heats with increasing altitude, the lapse rate may be expressed as a positive number. | Lapse rates are usually expressed as the amount of temperature change associated with a specified amount of altitude change, such as 9.8 [[Kelvin|K]] per [[kilometre]], 0.0098 K per [[metre]] or the equivalent 5.4 [[Fahrenheit and Rankine temperatures|°F]] per 1000 [[U.S. customary units|feet]]. If the atmospheric air cools with increasing altitude, the lapse rate may be expressed as a negative number. If the air heats with increasing altitude, the lapse rate may be expressed as a positive number. | ||
The lapse rate is most often denoted by the [[Greek alphabet|Greek]] capital letter Gamma, <font style="vertical-align:-5%;"><math>\scriptstyle\Gamma</math></font> or Γ,<ref><font style="vertical-align:-5%;"><math>\scriptstyle\Gamma</math></font> is the | The lapse rate is most often denoted by the [[Greek alphabet|Greek]] capital letter Gamma, <font style="vertical-align:-5%;"><math>\scriptstyle\Gamma</math></font> or Γ,<ref><font style="vertical-align:-5%;"><math>\scriptstyle\Gamma</math></font> is the LaTeX rendition and Γ is the HTML rendition.</ref> but not always. For example, the [[U.S. Standard Atmosphere]] uses L to denote lapse rates:<ref name=StdAtm>[http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770009539_1977009539.pdf U.S. Standard Atmosphere, 1976]</ref> A few others use the Greek lower case letter gamma, <font style="vertical-align:-10%;"> <math>\scriptstyle\gamma</math></font>, which is an unfortunate choice since gamma is also used for the [[specific heat ratio]]. | ||
== Types of lapse rates == | == Types of lapse rates == | ||
| Line 18: | Line 18: | ||
Earth's atmospheric air is rarely completely dry. It usually contains some [[water]] vapor and when it contains as much water vapor as it is capable of, it is referred to as saturated air (i.e., it has a [[relative humidity]] of 100%). The '''''dry adiabatic lapse rate''''' refers to the lapse rate of unsaturated air (i.e., air with a relative humidity of less than 100%). It is also often referred to as the ''dry adiabat'', ''DALR'' or ''unsaturated lapse rate''. It should be noted that the word ''dry'' in this context simply means that no liquid water (i.e., moisture) is present in the air ... water vapor may be and usually is present. | Earth's atmospheric air is rarely completely dry. It usually contains some [[water]] vapor and when it contains as much water vapor as it is capable of, it is referred to as saturated air (i.e., it has a [[relative humidity]] of 100%). The '''''dry adiabatic lapse rate''''' refers to the lapse rate of unsaturated air (i.e., air with a relative humidity of less than 100%). It is also often referred to as the ''dry adiabat'', ''DALR'' or ''unsaturated lapse rate''. It should be noted that the word ''dry'' in this context simply means that no liquid water (i.e., moisture) is present in the air ... water vapor may be and usually is present. | ||
The dry adiabatic lapse rate can be mathematically expressed as:<ref>{{cite book|author=John E. Frederick|title=Principles of Atmospheric Science|edition=1st Edition|publisher=Jones and Bartlett|year=2008|id=ISBN 0-7637-4089-6}}</ref> | The dry adiabatic lapse rate can be mathematically expressed as:<ref>{{cite book|author=John E. Frederick|title=Principles of Atmospheric Science|edition=1st Edition|publisher=Jones and Bartlett|year=2008|id=ISBN 0-7637-4089-6}}</ref><ref>[http://amsglossary.allenpress.com/glossary/search?p=1&query=dry-adiabatic+lapse&submit=Search Glossary of Meteorology] Dry adiabatic lapse rate from the glossary of the [[American Meteorological Society]]</ref> | ||
:<math>\Gamma_d = \frac{g}{c_{pd}}</math> | :<math>\Gamma_d = \frac{g}{c_{pd}}</math> | ||
| Line 40: | Line 40: | ||
=== Wet adiabatic lapse rate === | === Wet adiabatic lapse rate === | ||
An unsaturated parcel of air will rise from Earth's surface and cool at the dry adiabatic rate of – 9.8 K/kilometre (5.4 °F/1000 ft) until it has cooled to the temperature, known as the ''[[ | An unsaturated parcel of air will rise from Earth's surface and cool at the dry adiabatic rate of – 9.8 K/kilometre (5.4 °F/1000 ft) until it has cooled to the temperature, known as the ''atmospheric [[dew point]]'', at which the water vapor it contains begins to condense (i.e., change phase from vapor to liquid) and release the latent [[heat of vaporization]]. At that dew point temperature, the air parcel is saturated and, because of the release of the heat of vaporization, the rate of cooling will decrease to what is known as the '''''wet adiabatic lapse rate'''''. This rate is also often referred to as the ''wet adiabat'', ''saturated lapse rate'', ''SALR'', ''moist adiabatic lapse rate'' or ''MALR''.<ref name=EPA/><ref name=Woodruff/> | ||
The wet adiabatic lapse rate is not a constant since it depends upon how much water vapor the atmospheric air contained when it started to rise, which means the amount of heat of vaporization available for release is variable. In the troposphere, the rate can vary from about 4 K/kilometre (2.2 °F/1000 ft) in regions where the ambient temperature is about 25 °C (77 °F) to about 7 K/kilometre (3.8 °F/1000 ft) in regions where the ambient temperature is about – 10 °C (14 °F). | The wet adiabatic lapse rate is not a constant since it depends upon how much water vapor the atmospheric air contained when it started to rise, which means the amount of heat of vaporization available for release is variable. In the troposphere, the rate can vary from about 4 K/kilometre (2.2 °F/1000 ft) in regions where the ambient temperature is about 25 °C (77 °F) to about 7 K/kilometre (3.8 °F/1000 ft) in regions where the ambient temperature is about – 10 °C (14 °F). | ||
| Line 46: | Line 46: | ||
After the air parcel has reached its dew point and cooling has decreased to the wet adiabatic lapse rate, it will eventually rise to a point where all of its water vapor has condensed and its rate of cooling will then revert back to the dry adiabatic lapse rate. | After the air parcel has reached its dew point and cooling has decreased to the wet adiabatic lapse rate, it will eventually rise to a point where all of its water vapor has condensed and its rate of cooling will then revert back to the dry adiabatic lapse rate. | ||
The wet adiabatic lapse rate can be mathematically expressed as:<ref>[http://amsglossary.allenpress.com/glossary/search?p=1&query=moist-adiabatic+lapse&submit=Search Glossary of Meteorology] | The wet adiabatic lapse rate can be mathematically expressed as:<ref>[http://amsglossary.allenpress.com/glossary/search?p=1&query=moist-adiabatic+lapse&submit=Search Glossary of Meteorology] Moist adiabatic lapse rate from the glossary of the American Meteorological Society</ref> | ||
<math>\Gamma_w = g\, \frac{1 + \dfrac{H_v\, r}{R_{sd}\, T}}{c_{p d} + \dfrac{H_v^2\, r\, \epsilon}{R_{sd}\, T^2}}</math> | :<math>\Gamma_w = g\, \frac{1 + \dfrac{H_v\, r}{R_{sd}\, T}}{c_{p d} + \dfrac{H_v^2\, r\, \epsilon}{R_{sd}\, T^2}}</math> | ||
{|border="0" cellpadding="2" | {|border="0" cellpadding="2" | ||
| Line 89: | Line 89: | ||
|align=right|<font style="vertical-align:-30%;"><math>c_{pd}</math></font> | |align=right|<font style="vertical-align:-30%;"><math>c_{pd}</math></font> | ||
|align=left|= The specific heat of dry air at constant pressure, J/(kg <math>\cdot</math> K) | |align=left|= The specific heat of dry air at constant pressure, J/(kg <math>\cdot</math> K) | ||
|} | |||
{| border="0" width="320" align="right" cellpadding="0" cellspacing="0" style="wrap=no" | |||
| | |||
{| class = "wikitable" align="right" | |||
|+ U.S. Standard Atmosphere<br/>Lapse Rates | |||
!Altitude Region<br/>(m)!!Lapse rate<br/>(K/km)!!Lapse rate<br/> °F/1000 feet | |||
|- align="center" | |||
|0.00 to 10,999||-6.5||-3.566 | |||
|- align="center" | |||
|11,000 to 19,999||0.0||0.000 | |||
|- align="center" | |||
|20,000 to 31,999||1.0||0.549 | |||
|- align="center" | |||
|32,000 to 46,999||2.8||1.536 | |||
|- align="center" | |||
|47,000 to 50,999||0.0||0.000 | |||
|- align="center" | |||
|51,000 to 70,999||-2.8||-1.536 | |||
|- align="center" | |||
|71,000 to 85,000||-2.0||-1.092 | |||
|} | |||
|} | |} | ||
=== Environmental lapse rate === | === Environmental lapse rate === | ||
The dry adiabatic lapse rate and the wet adiabatic lapse rate are both theoretical rates. The actual real-world profile of temperature versus altitude that exists at any given time and in any given geographical location is called the '''''environmental lapse rate''''', also often referred to as the ''ELR'', ''prevailing lapse rate'' or ''ambient lapse rate''.<ref name=EPA/><ref name=Woodruff/><ref name=Beychok>{{cite book|author=Milton R. Beychok|title=Fundamentals of Stack Gas Dispersion|edition=4th Edition|publisher=Milton R. Beychok|year=2005|id=ISBN 0-9644588-0-2}}</ref> | The dry adiabatic lapse rate and the wet adiabatic lapse rate are both theoretical rates. The actual real-world profile of temperature versus altitude that exists at any given time and in any given geographical location is called the '''''environmental lapse rate''''', also often referred to as the ''ELR'', ''prevailing lapse rate'' or ''ambient lapse rate''.<ref name=EPA/><ref name=Woodruff/><ref name=Beychok>{{cite book|author=Milton R. Beychok|title=[[Fundamentals of Stack Gas Dispersion]]|edition=4th Edition|publisher=Milton R. Beychok|year=2005|id=ISBN 0-9644588-0-2}}</ref> | ||
[[Meteorology|Meteorologist]]s measure vertical temperature profiles by releasing weather balloons with mini-weather stations attached to them called [[radiosonde]]s. Sometimes, meteorologists drop these mini-weather stations from an airplane at high altitude with a parachute attached. This type of measuring device is called a [[dropsonde]]. | |||
In general, the ambient atmospheric air in the troposphere decreases with increasing altitude and so the environmental lapse rate is denoted as being negative. A committee consisting of 29 organizations and universities in the [[United States of America]], established an average environmental lapse rate named the [[U.S. Standard Atmosphere]]<ref name=StdAtm/> having various values, as shown in the adjacent table, which are dependent on the altitude region of Earth's atmosphere. From the Earth's surface to an altitude of 11 kilometres, the value of the U.S. Standard Atmosphere is – 6.5 K/km (3.57 °F/1000 feet). | |||
A number of other organizations have established "Standard Atmospheres", including the [[International Civil Aviation Organization]] (ICAO)<ref>''Manual of the ICAO standard atmosphere extended to 80 kilometres (50 miles)'', Document 7488-CD, Third Edition, 1993</ref>, the [[International Organization for Standardization]] (ISO)<ref>''Standard Atmosphere'', ISO 2533:1975/Add2:1997</ref> and the [[World Meteorological Organization]] (WMO), all three of whom agree with the U.S. Standard Atmosphere for altitudes up to 11 km (6.8 miles) | |||
{| border="0" width="375" align="right" cellpadding="0" cellspacing="0" style="wrap=no" | |||
| | |||
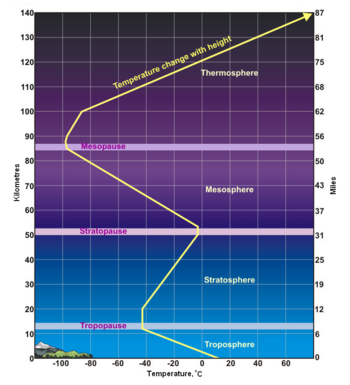
|{{Image|AtmTempProfile.png|right|350px|Temperature versus altitude within the Earth's atmosphere.}} | |||
|} | |||
The adjacent graph, published by the United States [[National Weather Service]] (NWS),<ref>[http://www.srh.noaa.gov/srh/jetstream/atmos/layers.htm The Layers of the Atmosphere] From the website of the [[National Oceanic and Atmospheric Administration]] (NOAA) and the [[National Weather Service]] (NWS)</ref> depicts the average profile of temperature versus altitude in the various layers the Earth's atmosphere. As can be seen, it is generally in fair agreement with the above tabulated lapse rates of the U.S. Standard Atmosphere. | |||
At times, ''[[inversion layer]]s'' may form in the troposphere. Such inversion layers will have a positive environmental lapse rate, meaning that the atmospheric temperature increases with altitude within the inversion layers<ref name=Beychok/>. An inversion layer may be one of two types: | At times, ''[[inversion layer]]s'' may form in the troposphere. Such inversion layers will have a positive environmental lapse rate, meaning that the atmospheric temperature increases with altitude within the inversion layers<ref name=Beychok/>. An inversion layer may be one of two types: | ||
Revision as of 10:44, 2 February 2023
- See also: Earth's atmosphere
The atmospheric lapse rate ( ) refers to the change of an atmospheric variable with a change of altitude, the variable being temperature unless specified otherwise (such as pressure, density or humidity).[1][2][3] While usually applied to Earth's atmosphere, the concept of lapse rates can be extended to atmospheres (if any) that exist on other planets.
Lapse rates are usually expressed as the amount of temperature change associated with a specified amount of altitude change, such as 9.8 K per kilometre, 0.0098 K per metre or the equivalent 5.4 °F per 1000 feet. If the atmospheric air cools with increasing altitude, the lapse rate may be expressed as a negative number. If the air heats with increasing altitude, the lapse rate may be expressed as a positive number.
The lapse rate is most often denoted by the Greek capital letter Gamma, or Γ,[4] but not always. For example, the U.S. Standard Atmosphere uses L to denote lapse rates:[5] A few others use the Greek lower case letter gamma, , which is an unfortunate choice since gamma is also used for the specific heat ratio.
Types of lapse rates
There are three types of lapse rates that are used to express the rate of temperature change with a change in altitude, namely the dry adiabatic lapse rate, the wet adiabatic lapse rate and the environmental lapse rate.
Dry adiabatic lapse rate
Since the atmospheric pressure decreases with altitude (see Earth's atmosphere), the volume of an air parcel expands as it rises. Conversely, if a parcel of air sinks from a higher altitude to a lower altitude, its volume is compressed by the higher pressure at the lower altitude. An adiabatic lapse rate is the rate at which the temperature of an air parcel changes in response to the expansion or compression process associated with a change in altitude, under the assumption that the process is adiabatic (meaning that no heat is added or lost during the process).[6][7]
Earth's atmospheric air is rarely completely dry. It usually contains some water vapor and when it contains as much water vapor as it is capable of, it is referred to as saturated air (i.e., it has a relative humidity of 100%). The dry adiabatic lapse rate refers to the lapse rate of unsaturated air (i.e., air with a relative humidity of less than 100%). It is also often referred to as the dry adiabat, DALR or unsaturated lapse rate. It should be noted that the word dry in this context simply means that no liquid water (i.e., moisture) is present in the air ... water vapor may be and usually is present.
The dry adiabatic lapse rate can be mathematically expressed as:[8][9]
| where: | |
| = the dry adiabatic lapse rate, 0.0098 K/m (equivalent to 9.8 K/kilometre or 5.4 °F/1000 feet) | |
| = Earth's gravitational acceleration, 9.8076 m/s2 | |
| = the specific heat of dry air at constant pressure, 1004.64 J/(kg K) |
The troposphere is the lowest layer of the Earth's atmosphere. Since and vary little with altitude, the dry adiabatic lapse rate is approximately constant in the troposphere.
Wet adiabatic lapse rate
An unsaturated parcel of air will rise from Earth's surface and cool at the dry adiabatic rate of – 9.8 K/kilometre (5.4 °F/1000 ft) until it has cooled to the temperature, known as the atmospheric dew point, at which the water vapor it contains begins to condense (i.e., change phase from vapor to liquid) and release the latent heat of vaporization. At that dew point temperature, the air parcel is saturated and, because of the release of the heat of vaporization, the rate of cooling will decrease to what is known as the wet adiabatic lapse rate. This rate is also often referred to as the wet adiabat, saturated lapse rate, SALR, moist adiabatic lapse rate or MALR.[6][7]
The wet adiabatic lapse rate is not a constant since it depends upon how much water vapor the atmospheric air contained when it started to rise, which means the amount of heat of vaporization available for release is variable. In the troposphere, the rate can vary from about 4 K/kilometre (2.2 °F/1000 ft) in regions where the ambient temperature is about 25 °C (77 °F) to about 7 K/kilometre (3.8 °F/1000 ft) in regions where the ambient temperature is about – 10 °C (14 °F).
After the air parcel has reached its dew point and cooling has decreased to the wet adiabatic lapse rate, it will eventually rise to a point where all of its water vapor has condensed and its rate of cooling will then revert back to the dry adiabatic lapse rate.
The wet adiabatic lapse rate can be mathematically expressed as:[10]
| where: | |
| = Wet adiabatic lapse rate, K/m | |
| = Earth's gravitational acceleration = 9.8076 m/s2 | |
| = Heat of vaporization of water, J/kg | |
| = The ratio of the mass of water vapor to the mass of dry air, kg/kg | |
| = The universal gas constant = 8,314 J/(kmol K) | |
| = The molecular weight of any specific gas, kg/kmol = 28.964 for dry air and 18.015 for water vapor | |
| = The specific gas constant of a gas, denoted as | |
| = Specific gas constant of dry air = 287 J/(kg K) | |
| = Specific gas constant of water vapor = 462 J/(kg K) | |
| =The dimensionless ratio of the specific gas constant of dry air to the specific gas constant for water vapor = 0.6220 | |
| = Temperature of the saturated air, K | |
| = The specific heat of dry air at constant pressure, J/(kg K) |
|
Environmental lapse rate
The dry adiabatic lapse rate and the wet adiabatic lapse rate are both theoretical rates. The actual real-world profile of temperature versus altitude that exists at any given time and in any given geographical location is called the environmental lapse rate, also often referred to as the ELR, prevailing lapse rate or ambient lapse rate.[6][7][11]
Meteorologists measure vertical temperature profiles by releasing weather balloons with mini-weather stations attached to them called radiosondes. Sometimes, meteorologists drop these mini-weather stations from an airplane at high altitude with a parachute attached. This type of measuring device is called a dropsonde.
In general, the ambient atmospheric air in the troposphere decreases with increasing altitude and so the environmental lapse rate is denoted as being negative. A committee consisting of 29 organizations and universities in the United States of America, established an average environmental lapse rate named the U.S. Standard Atmosphere[5] having various values, as shown in the adjacent table, which are dependent on the altitude region of Earth's atmosphere. From the Earth's surface to an altitude of 11 kilometres, the value of the U.S. Standard Atmosphere is – 6.5 K/km (3.57 °F/1000 feet).
A number of other organizations have established "Standard Atmospheres", including the International Civil Aviation Organization (ICAO)[12], the International Organization for Standardization (ISO)[13] and the World Meteorological Organization (WMO), all three of whom agree with the U.S. Standard Atmosphere for altitudes up to 11 km (6.8 miles)
The adjacent graph, published by the United States National Weather Service (NWS),[14] depicts the average profile of temperature versus altitude in the various layers the Earth's atmosphere. As can be seen, it is generally in fair agreement with the above tabulated lapse rates of the U.S. Standard Atmosphere.
At times, inversion layers may form in the troposphere. Such inversion layers will have a positive environmental lapse rate, meaning that the atmospheric temperature increases with altitude within the inversion layers[11]. An inversion layer may be one of two types:
- Surface inversion layer
- During the night, the Earth's surface loses heat rather rapidly by radiation while the ambient air above the surface looses heat more slowly by convection. Thus, what is called a radiation inversion forms in which the air temperature for some distance above the ground is higher than the air temperature very near to the ground. In other words, the environmental lapse rate within the surface inversion layer is positive and increases with altitude. Air very near Earth's surface which has flowed across a cold surface (such as a lake), and been cooled by advection, may also form a surface inversion layer called an advective inversion. Advection is a meteorological term for heat transfer occurring from horizontal air motion.[11]
- Inversion aloft
- During a typical diurnal pattern (i.e., daily cycle), the base of a radiation inversion formed during the night rises during the day as the Earth's surface warms up. As it rises, it forms what is called an inversion aloft. The base of that inversion aloft is a ceiling or lid, above which very little or essentially no vertical turbulence (i.e., vertical motion) or vertical mixing occurs within the inversion layer. The height of the lid is called the mixing height. As the day goes on and the Earth's surface continues to warm, the base of the inversion rises, the inversion layer gets thinner and the mixing height increases. When the base of the layer reaches the inversion top, perhaps by mid-afternoon on a hot summer day, the inversion aloft breaks up completely and the mixing height is no longer limited.[11]
Lapse rates and atmospheric stability
Atmospheric stability is a term used to qualitatively describe the amount of vertical motion of the air in the lower atmosphere (the troposphere). In broad general terms, the atmospheric stability can be characterized by these four categories:[6][7][11]
- A very stable atmosphere is one that has very little, if any, vertical motion of the air.
- A stable atmosphere is one that discourages vertical motion but does have some motion of the air.
- An unstable atmosphere is one that encourages continual vertical motion of the air, upwards or downwards.
- A neutral atmosphere is one that neither discourages nor encourages vertical motion of the air and is often referred to as conditionally stable.
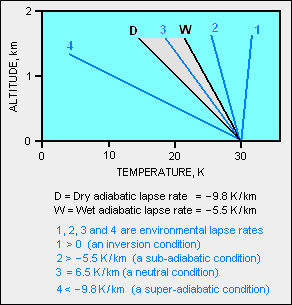
The numerical value of the environmental lapse rate determines the stability category of the atmospheric air. Referring to the adjacent diagram:
- If the environmental lapse rate (i.e., the actual ambient temperature gradient) is greater than zero as for the rate marked 1 in the diagram, then an inversion layer is present and the atmospheric temperature increases with altitude. There is essentially no vertical turbulence and the atmosphere is said to be very stable or extremely stable.
- If the environmental lapse rate is greater than – 5.5 K/km as for the rate marked 2 in the diagram, then there is some small amount of vertical turbulence and the atmosphere is said to be stable. It is also referred to as being sub-adiabatic.
- If the environmental lapse rate lies between the wet adiabatic lapse rate and the dry adiabatic lapse rate as for the rate marked 3 in the diagram, then the atmosphere is said to be neutral. That designation would apply to the U.S. Standard Atmosphere of – 6.5 K/km in most cases.[15]
- If the environmental lapse rate is less than the dry adiabatic lapse rate as for the line marked 4 in the diagram, then there turbulence in the atmosphere and it is said to be unstable. It is also referred to as being super-adiabatic.
- Although not shown in the diagram, if the environmental lapse rate were zero (perfectly vertical), then the atmosphere would be in an isothermal condition (no change of temperature with altitude) and would be also be said to be very stable.
Importance of understanding atmospheric stability
An understanding and knowledge of atmospheric stability is important for many reasons. What follows is a brief discussion of some of those reasons:
Probably one of the most important reasons is that atmospheric turbulence and mixing plays a major role in air pollution dispersion modeling. Turbulence and mixing is provided by an unstable atmosphere and thus enhances the dispersion of air pollutant, while a stable atmosphere inhibits turbulence and results in very poor dispersion of air pollutants.[11]
A stable atmosphere inhibits rain fall, while an unstable atmosphere encourages rainfall and thunderstorms.[16][17] A stable atmosphere also inhibits forest fire activity and an understanding of atmospheric stability helps explain certain aspects of forest fire behavior.[18]
A certain amount of atmospheric instability is important for glider pilots, since without it the thermals needed for glider flight would not form. Understanding of atmospheric stability is also important for the safety of glider pilots because high atmospheric instability may lead to thunderstorms.[19]
The atmospheric stability has a large impact on the deposition and drift of aerially applied sprays of various farm crop protection materials.[20]
References
- ↑ The lapse rate is often defined as the negative change of temperature with a change of altitude. That definition leads to statements such as "A positive lapse rate indicates cooling as height increases while a negative lapse rate indicates warming as height increases". That is counter-intuitive since lapse rates are usually denoted as a negative number (i.e., – 6.5 K/kilometre or the equivalent 3.6 °F/1000 feet) to indicate cooling with an increase of height.
- ↑ Lapse rates and air parcels Professor Robert Fovell, Department of Atmospheric and Oceanic Science, University of California, Los Angeles
- ↑ Characteristics of Air Parcels and Air Masses; Clouds Dr. Nicholas Short, National Aeronautics and Space Administration (NASA)
- ↑ is the LaTeX rendition and Γ is the HTML rendition.
- ↑ 5.0 5.1 U.S. Standard Atmosphere, 1976
- ↑ 6.0 6.1 6.2 6.3 Vertical Motion and Atmospheric Stability From the website of the U.S. Environmental Protection Agency
- ↑ 7.0 7.1 7.2 7.3 About Atmospheric Stability Steve W. Woodruff, Pierce College, Los Angeles, California.
- ↑ John E. Frederick (2008). Principles of Atmospheric Science, 1st Edition. Jones and Bartlett. ISBN 0-7637-4089-6.
- ↑ Glossary of Meteorology Dry adiabatic lapse rate from the glossary of the American Meteorological Society
- ↑ Glossary of Meteorology Moist adiabatic lapse rate from the glossary of the American Meteorological Society
- ↑ 11.0 11.1 11.2 11.3 11.4 11.5 Milton R. Beychok (2005). Fundamentals of Stack Gas Dispersion, 4th Edition. Milton R. Beychok. ISBN 0-9644588-0-2.
- ↑ Manual of the ICAO standard atmosphere extended to 80 kilometres (50 miles), Document 7488-CD, Third Edition, 1993
- ↑ Standard Atmosphere, ISO 2533:1975/Add2:1997
- ↑ The Layers of the Atmosphere From the website of the National Oceanic and Atmospheric Administration (NOAA) and the National Weather Service (NWS)
- ↑ Since the wet adiabatic lapse rate may be as low as – 4 K / km, the U.S. Standard Atmosphere may not always lie between the wet and dry adiabatic lapse rates
- ↑ Atmospheric Stability and Instability From the website of the Utah State University
- ↑ Atmospheric Stability
- ↑ Atmospheric stability From the website of the Encyclopedia of Southern Fire Science (ESFS)
- ↑ Federal Aviation Administration (2007). Glider Flying Handbook, Reprint Edition. Skyhorse Publishing. ISBN 1-60239-061-4.
- ↑ Role of Atmospheric Stability in Drift and Deposition of Aerially Applied Sprays – Preliminary Results 2004 Annual Meeting, American Society of Agricultural and Biological Engineers