In physics, angular momentum is a kinematic property of a system consisting of one or more point masses. Its importance derives from the fact that it is conserved in several physical circumstances. (Recall that a conserved property of a system is one that does not change over time.)
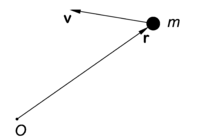
Point mass
m with velocity
v has angular momentum
L ≡
m r ×
v with respect to
O.
L is a vector pointing towards the reader
Definition
The angular momentum of a single point mass m is defined with respect to a point O. Denote the vector from O to m by r (see the figure). Let the mass have velocity v, then
the angular momentum L of the point mass is defined as the cross product,

It follows from the definition of cross product that the vector L is perpendicular to the plane of the figure and points towards the reader. Note that the definition p ≡ m v for the linear momentum is introduced here.
The definition of the angular momentum of a system of n point masses is the following simple generalization:

Conservation of angular momentum
For simplicity we consider the case of one point mass, generalization to n point masses is straightforward. The following important result will be proved: a particle that moves in a centrally symmetric potential has a conserved angular momentum.
Using Newton's dot (fluxion) notation for time derivatives, we find

Use

where we invoked Newton's second law
 Hence the time derivative of the angular momentum is equal to the torque N,
Hence the time derivative of the angular momentum is equal to the torque N,

It follows that the angular momentum is conserved—i.e., its time derivative is zero—if the applied torque N is zero, which means that either F is zero, or r and F are parallel, because in that case the cross product vanishes.
The former case occurs when the mass moves uniformly in homogeneous space (no external forces). Then also the linear momentum of the point mass is conserved, and therefore one rarely considers the angular momentum in the case of uniform rectilinear motion.
The second case is more interesting. Let us assume that F is conservative, i.e., its curl vanishes, then F is the gradient ∇ of a potential V(x,y,z),

so that for a conservative force the time derivative of L is

The quantity in brackets is known in group theory as a Lie derivative of the full rotation group SO(3). In quantum mechanics it is a well-known operator, namely the orbital angular momentum operator (except for the factor  ).
).
From the general properties of Lie derivatives—or equivalently orbital angular momenta—it follows that the time derivative of L vanishes whenever the potential V(x,y,z) is rotationally invariant (isotropic, central-symmetric). This means that the function V(x,y,z) depends on r only, when expressed in spherical polar coordinates (r, θ, φ). By expressing the gradient ∇ in spherical polar coordinates and writing the cross product as a determinant, we can prove this explicitly, using that the derivatives of V with respect to θ and φ are zero,

A well-known example is the motion of the earth around the sun. To a very good approximation the gravitation is central-symmetric (rotationally invariant) and hence the earth's orbit is characterized by a conserved angular momentum. Kepler's second law is a direct consequence of this conservation of angular momentum.
Generalization to n point masses
When in a system of n point masses the particles do not interact mutually, the generalization is simply

where the forces F i are external. If the total external torque is zero, the total angular momentum of the system is conserved.
When the particles do interact, i.e., there are non-zero internal forces, then the result still holds, provided the internal forces are central-symmetric and additive. No internal torque occurs in that case. In order to show this, we recall that Newton's third law (action = −reaction) holds for central-symmetric forces. Indicating internal forces by a double suffix, we write Newton's law as follows,

where the left hand side is the force on particle i executed by particle j and the right hand side is i acting on j. Both forces act along the vector pointing form particle i to j,

so that

where

The total internal torque on particle i is,

Under assumption of additivity, the total internal torque can be written as

and

where F i (characterized by a single suffix) is external.
Separation of center of mass
The angular momentum of a system of point masses with respect to an arbitrary point O can be separated into two terms. The first term is the angular momentum with respect to O of a particle with total mass M positioned at the center of mass C of the system. The other term is the sum of the angular momenta of the particles with respect to C.
The center of mass C is determined by

Introduce s i for particle i at point P i

Note that

and hence also

Now,

where the two cross terms vanished and the two diagonal terms are non-vanishing. The two remaining terms are:

If the total system moves in homogeneous (field free) space, the first term is conserved and is usually not of much interest. The second term, the sum of the angular momenta of the n particles with respect to the center of mass, is usually designated the total angular momentum of the system,

where the position vectors s i are defined with respect to a system of axes with origin in the center of mass C of the system.
Circular motion around a fixed axis
A system often encountered in physics is a particle (point mass) that moves along a circle in a fixed plane. Let us choose a system of axes such that the plane of motion is the x-y plane, with the z-axis perpendicular to the plane.
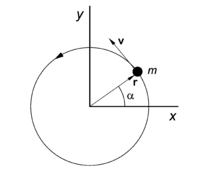
Point mass
m with instantaneous velocity
v moves counterclock-wise on circle.
The coordinates of the particle and its time derivative are

where we used that the radius r of the circle is time-independent. The angular momentum is given by

The quantity mr 2 is the inertia moment I of the present simple system (particle on a circle) and ω is the angular velocity. The angular velocity, as defined here, is a scalar. Often the product ωez is defined as angular velocity ω, which is a vector.
In summary, for a particle moving on a circle around a fixed axis, the angular momentum is proportional to the angular velocity with the inertia moment as proportionality factor,

It is of some interest to point out that this simple relation becomes a vector-tensor relation for more general motions of more general systems (rigid rotors) for which the rotational axis is not fixed in space: L and ω remain vectors, but the inertia moment generalizes to a second rank, symmetric, tensor.
Angular momentum of a rigid body; inertia moment
Angular velocity of a rigid body
We consider a system of n point masses (particles) with fixed—time-independent—relative positions. The position vectors r i(t) are all with respect to a laboratory-fixed frame with origin in the center of mass of the system. The lengths of the n vectors and the angles between them are all time-independent, because the system is rigid. We will prove the following expression for the time derivatives of the position vectors,

where the vector ω is a 3-vector which is the same for all n particles, it is the angular velocity of the rigid body.
The time dependence of the position vectors of a rigid body has the following matrix-vector form

The vectors r i(0) determine the shape of the rigid body at time zero. This shape is invariant since all inner products are time-independent. Indeed,

We used here the equivalent notations, valid for any two vectors of the same dimension,

where the notation on the right hand side is based on the fact that column and row vectors are rectangular matrices. Further we used the matrix transposition rule,

Differentiation with respect to time gives

and hence the matrix product  is equal to an antisymmetric matrix. A 3×3 antisymmetric matrix is parametrized by three real numbers and has the following form,
is equal to an antisymmetric matrix. A 3×3 antisymmetric matrix is parametrized by three real numbers and has the following form,

Differentiation of a position vector with respect to time, followed by insertion of the identity matrix gives,

where the vector ω is composed of the matrix elements of the antisymmetric matrix,

The fact that the matrix-vector multiplication may be written as a cross product follows most easily by direct verification. This proves the desired result.







































